Four Methods for Adding Fractions
One of the greatest struggles for a middle school math teacher is helping your students understand fractions. One of the reasons for this struggle is that students have a hard time visualizing fractions being added. (Another reason is our inability to do basic multiplication - but that is a different story). In this article we are looking at four different ways to teach adding fractions.
Method #1 - The Traditional Stacking Method
This is the method that most of us were taught add fractions. It requires that students understand multiples which can be a struggle for some of our students.
Step one
The first method (and probably the most common) is stacking the two fractions you are adding and then finding the common denominator. In the example above we are adding 3/5 + 1/4. One method of finding a Common Denominator is to find the multiples of both denominators and circle the smallest number shared (least common). Another method to multiply the two denominators (5 x 4). This will also give you a common denominator (but, it may not be the least common)
Step two
Create a proportion using the common denominator (the number 20 in orange in picture above).
Step three
The next method is to solve the proportion to find the numerator. Our preferred method is to cross multiply (20 x 3) and then divide by 5 which gives us 12 as our new numerator. (The other proportion equals 5). See example above.
Step four
The final step is to add up the numerators (12 + 5 = 17) and to keep the common numerator (20). The answer to 3/5 + 1/4 = 19/20
Method #2 - The Grid Method
This is a nice way to visualize adding fractions. All it requires is a sheet of paper, a couple of markers/highlighters, and something to place on the grid such as chips/blocks. It only takes a couple of minutes to set up and all the students can participate.
Step one
Give the students an addition problem such as 1/4 + 1/3. Have the students draw four (4) columns with one of the markers. and three rows with another color. The four columns and 3 rows are the two denominators we are using. We like to use different color markers to help students see the fourths and the thirds on the grid.
Step two
Next, fill in one of the four columns with your chips/blocks. We make sure that we reinforce how 3/12 and 1/4 are equivalent fractions.
Step three
Use a different color (green in this instance) chip to represent the fraction 1/3. Place the chips on one of the three rows. Once again we try to emphasis that 1/3 is equivalent to 4/12.
Step Four
You will notice that one of the "squares" has two chips. Just relocate one of the chips to an open square. The result is 7 of the 12 "squares are filled in or 7/12.
See other examples of the Criss Cross Method at: https://www.blogger.com/blogger.g?blogID=387842251510482837#editor/target=post;postID=162997258285854749;onPublishedMenu=allposts;onClosedMenu=allposts;postNum=3;src=postname
Method #3 - The Criss Cross Method
This is a method that we started using this past school year. It has been very helpful for students that really struggle with the traditional method of finding common denominator. One word of warning: often students will use this method when denominators are the same which is unneeded.
Step one
The first step of the criss cross method it to cross multiply. In the example above you would multiply 5 x 1 and 4 x 2 and put the answers above (the 5 and 8 in red).
Step two
The second step is to add these two numbers (5 & 8 in red). This will be your new numerator.
Step three
The final step is to multiply the Denominators (4 and 5 circled in green). The 20 is the new denominator.
Method #4 - The Ky Davis Model
This past fall we attended an inservice led by Ky Davis of Muskingum University who showed us this fourth method of adding fractions. This is not a method that we have found to be very practical for a middle school class, but it would be great for a young student first learning about fractions.
Step one
Lets say you are adding 1/3 + 1/4. The first thing you do is set up a fraction for 1/3 using tally marks (one tally on top and 3 tallies on the bottom). Next set up a fraction for 1/4 using tally marks (one tally on top and 4 tallies on the bottom).
Step two
The goal is to add tally marks to these fractions until the denominators are the same. This second step requires the student to add 1 tally mark to the numerator and three tally marks to the denominator. This will give you a fraction of 2/6 (which is equivalent to 1/3). At this point the denominators are still different.
Step three
The next step is to add 1 tally to the numerator and 4 tally marks to the denominator of the fraction 1/4. This gives you the fraction of 2/8 on the 1/4 side. The 1/4 denominator is now larger (6 to 8).
Step four
The students add another 1/3 (blue) to the left side of this problem. You now have a fraction that is 3/9 on the side with 1/3. The denominators are still different (9 to 8).
Step five
Next we add another 1/4 (light blue) to the right side fraction. The right side is now 3/12.
Step six
The students will now add another 1/3 to the left side fraction (red). That makes the total on the left side 4/12. At this point both sides have 12 tallies in the denominator. The left side (the original 1/3) is now 4/12 and the right side (original right side) is now 3/12.
Step seven
Finally, add up the total of tally marks in the numerator (in this situation the numerator = 7). Keep the amount tallies in one of the fractions (12). The final answer is 1/3 + 1/4 = 7/12.
Todd Hawk is a middle school math teacher and the co-founder of the Land of Math website (www.landofmath.com). You can reach him at landofmath2@gmail.com or follow him on twitter: @landofmath2












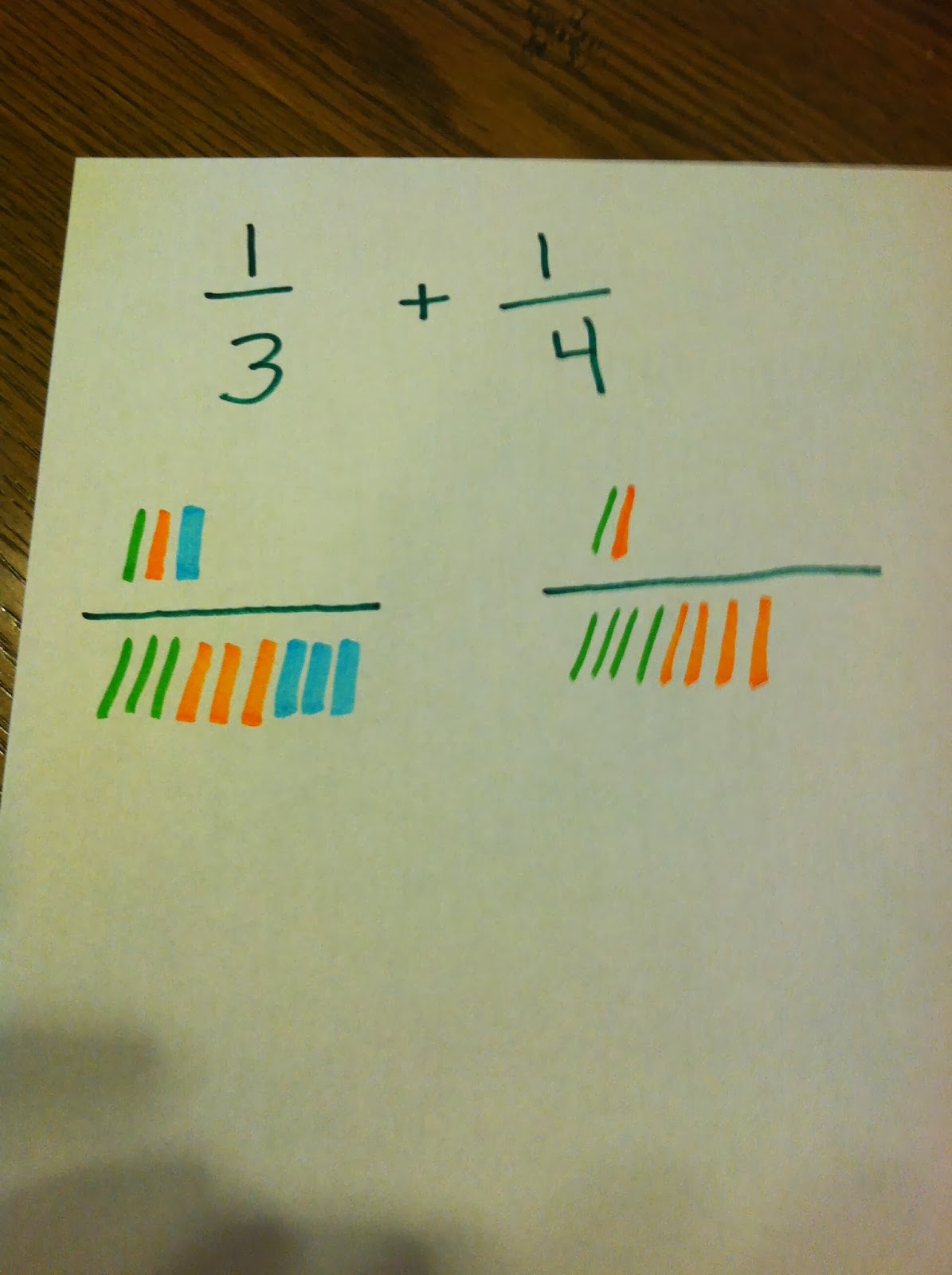



Nice work!
ReplyDelete